数学是从生产生活中诞生的,随着数学的发展,逐渐超出了人们的想象。虚数就是数学发展过程中的一个典型例子,不过,直到今天,仍有很多小伙伴对虚数表示难以理解。本文,就与您一起来聊聊虚数其实不虚。
一、现实中不应该存在的数
假设有一块边长为5米的正方形土地,现在想把这个土地扩大出39平方米并且仍旧是正方形。其实这个题目很简单,初中生应该都会,就是求方程(5+x)^2=25+39的根。最后得到的结果是x=3或x=-13。根据题意,可以得到x=3,因为边长不能是负数,所以-13是无效解。
如果前面这个例子还可以理解,那么下面这个方程就无法接受了。x^2+2x+2=0,为了求解x我们把方程变换一下(x+1)^2=-1。很明显,这个题目如果在实数范围内是做不下去的。什么数的平方会是负数呢?
这个能平方后能产生负数的方程曾经在很长一段时间里困扰着数学家们,莱布尼兹就曾经认为,这是数学解析中的一个奇异,在现实中的是不存在的,所以就把它称作了虚数。
二、现实中的虚数意义
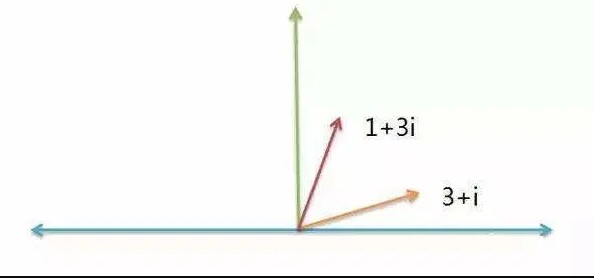
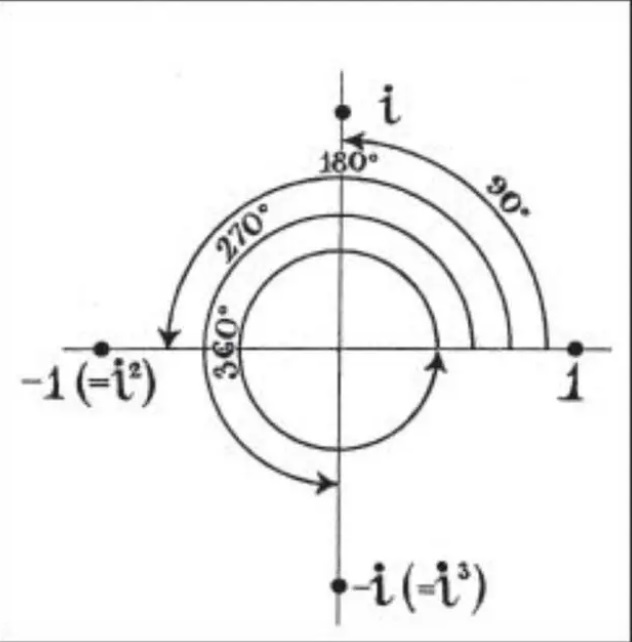
我们现在知道-1的平方根是i,让我们一起来探索一下i的性质。考虑在一根数轴上的实数,1、2、3……,如果把它们乘以-1就得到-1、-2、-3……。这些数相当于是原来那个数以原点为中心旋转180度。由于i^2=-1,这意味着,一个数两次乘以i旋转了180度。 换句话说,就是一个实数如果乘以一个i意味着旋转了90度。我们把一个实数乘以i之后的数叫做纯虚数,它位于与实数轴垂直的虚数轴上。方程x^2-6x+25=0有两个根,x=3±4i,这两个根就是在由实数数轴,以及与实数数轴垂直的虚数数轴构建的平面上的两个点相对应。我们把实数+实数i这种结构的数叫做复数。
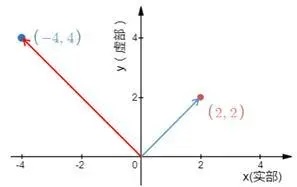
很明显,复数的这个特点意味着这是一个超越了只有正负两个方向的实数,是一个能描述平面上所有点的方向的更广义上的数。虚数i的意义就在于与实数一起构建了一个向量空间,复数描述了这个空间中的点距离原点的距离和离开实数正方向所偏转的角度。
对于一个复数z=a+bi,其距离原点的距离为r=(a^2+b^2)^(1/2),其偏转角度为θ,tanθ=b/a。r被称为z的绝对值,用|z|来表示,θ叫做z的辐角,用arcz表示。
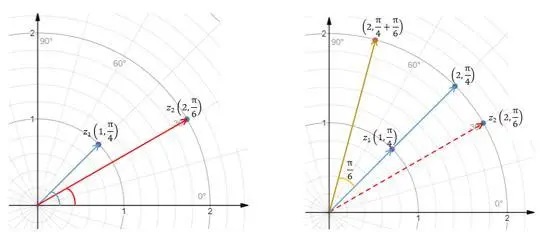
三、虚数(复数)与物理学 物理学中经常要计算质点的位移,有了复数这种处理就简单了很多。举个例子,某质点在t1时刻其复平面内的位置为r1=2+3i,t2时刻的位置为r2=5+3i,求t1、t2时刻中位移的变化Δr。其实也很简单,r2-r1=3。意味着,在这个时刻内,这个质点沿着实数轴的正方向移动了3个单位,而在虚数轴正方向位置保持不变。
由于不是数学内容,所以这里简单总结一下复数运算的物理意义。复数的加减法其实就是分别沿着实数轴和虚数轴的平移,而复数的乘除法其实就是复数的伸缩和旋转。正是因为复数的这种性质,所以复数很自然地被应用于物理学当中。
在GPS导航中,复数被用于计算和描述交通工具所处的位置及位置变化信息。由于复数不仅有大小(距离)而且还包含辐角,所以也被用于描述很多周期性的变化运动当中,尤其是在电磁学当中有着非常广泛的应用,后来更被应用于量子力学当中。
如今,复变函数是物理专业学生的基本计算技能,是物理系本科生,数学科目中的必修课。

选自:
https://baijiahao.baidu.com/s?id=1678770768559842987&wfr=spider&for=pc&searchword=%E8%99%9A%E6%95%B0%E7%9A%84%E5%BA%94%E7%94%A8%E5%AE%9E%E4%BE%8B
虚数对很多人来说都比较陌生,似乎很难以理解。而且最大的疑惑是,这个东西到底有没有实际意义呢?确实,我们在现实生活中从来没有遇到有什么东西是需要虚数的。
负数还算是容易理解的,如果我们需要还房贷,那么欠银行的钱就是负数,如果去商店买东西,钱如果不够,那么差的那部分钱就是负数,每月信用卡欠账是负数。但是,我们从来没有看到过什么东西是虚数的,没听说有人买了个东西花了100块钱,或者账本里记着一笔账是1万,这是非常诡异的事情。
我们对虚数的认识,似乎仅仅停留在数学课本中,仅仅是为了计算的方便而引入的一个数学符号。
17个改变世界的数学公式之虚数公式
我们把公式拿出来看一下,就是:或者是。
虚数是法国数学家笛卡尔(1596-1650)引入的,引入虚数的目的就是为了给负数开根号,这时候的也仅仅是一个数学符号而已。
法国数学家笛卡尔
但是让笛卡尔没有想到的是,自从他“发明”了虚数以后,虚数的前途就不可限量,在很多领域都展露出攻城略地的巨大力量,用德国数学家莱布尼茨(1646-1716)的话说就是:"虚数是美妙而奇异的神灵隐蔽所,它几乎是既存在又不存在的两栖物。”
后来,德国数学家高斯(1777-1855)又把实数与虚数结合起来,提出了复平面的概念,类似下面的坐标图: 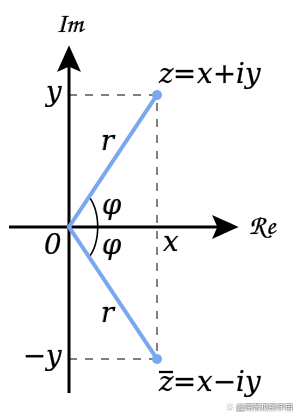 复数平面 就是复平面上的一个点,对于来说,既有实部,也有虚部,与纯粹的实数不同,也与纯粹的虚数不同,是一种复合的数,所以叫作“复数”。
在我们的日常生活中,能遇到这样的“复数”吗?似乎是没有,无论是去买东西,或者银行账户,或者财务账本里,都没有“复数”,没有人说这个东西的价格是元。
但是从物理的角度来看,我们会看到很多可以用复数表示的东西,这就是矢量,比如力是矢量,速度是矢量,加速度是矢量,还有看不见的电磁波也是矢量。如果是矢量,就可以把它放在复平面中用复数来表示,比如力,因为对矢量来说,就是有两个分量,一个是方向的分量,另一个是方向的分量 。
而这个时候的其实已经不是一个用来开根号的数学符号了,而是代表了在复平面上的旋转,例如,力矢量原来是在轴方向上的一个力,那么当与相乘就改变了方向,逆时针旋转变成轴方向上的力,如果再与相乘就变成,也就是与力大小相等,方向相反的一个力,相当于又逆时针旋转。
如果我们再继续旋转,就会有,如果再乘则继续逆时针旋转,变成回到了原来的地方。
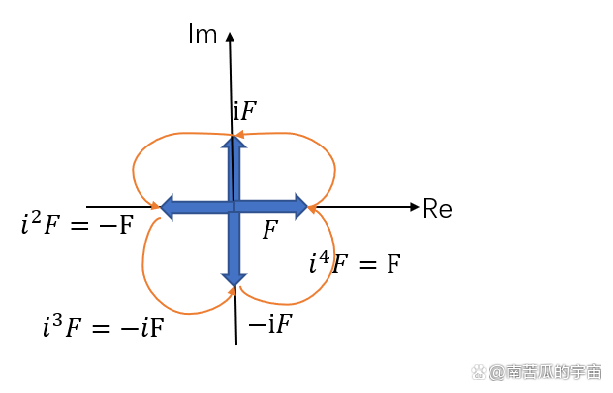
复数平面
参考:
https://baijiahao.baidu.com/s?id=1729866355241934619&wfr=spider&for=pc&searchword=%E7%94%A8%E5%A4%8D%E6%95%B0%E8%A1%A8%E7%A4%BA%E5%8A%9B
下期我们接着聊虚数。
上次我们初步把虚数是怎么来的做了介绍改变世界的17个公式之虚数的奇妙旅行(一),这次我们继续讲虚数,虚数的奇妙之旅才刚刚开始。
如果说,复数=实数+虚数,可以用来在物理上表示一些矢量,比如速度、力或者位移等,那么可就小看虚数了。当瑞士数学家欧拉(1707-1783)把虚数与三角公式联系在一起的时候,虚数的威力才真正被发挥出来了,这就是非常著名的欧拉公式。
欧拉公式 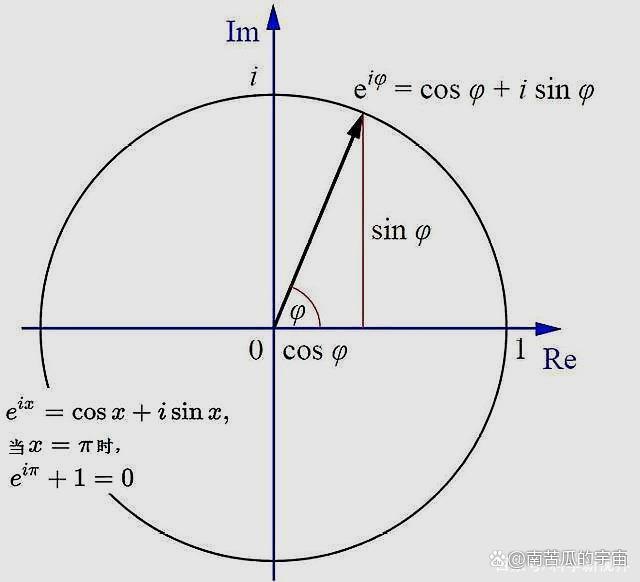
图中的欧拉公式 ,当的时候就会有: 。
也就是,此式被称作史上最美妙的数学公式之一,公式中汇集了自然常数,圆周率,自然数。
欧拉公式为我们在数学和物理上打开了一扇门,与牛顿的运动三定律、万有引力定律一样,是开天辟地的大事,从此科学发展的面貌焕然一新。
由于欧拉找到了虚数与三角函数之间的关系,虚数就真正地进入了物理学,不仅仅可以分析各类矢量,还可以对波进行分析,实部代表了波的幅度,虚部则代表了波的相位,很多非常复杂的物理现象就可以用复数来描述了,而且描述起来非常简约。
1926年,奥地利物理学家薛定谔(1887-1961)提出了量子力学的基本方程即薛定谔方程,由于薛定谔认为微观粒子可以被看成一种“波”,而波又可以用波函数来描述,且波函数中就用到了虚数,这样,虚数就名正言顺地进入了量子力学。
但是,虚数在量子力学中有真正的物理意义吗?很多人都怀疑虚数在微观粒子世界中的作用,难道还只是一个数学符号?
我们举例来说,比如在上世纪70年代的电磁力与弱力的统一理论中,正是由于规范场理论中复数(实数+虚数)的作用,才预言出新的传递弱力的玻色子W+、W-、Z0,同时把传递电磁力的光子也统一在群中,进而实现了电弱统一。
还有,2022年1月有个报道,也是关于复数的:
据中国科学技术大学消息,该校潘建伟、陆朝阳、朱晓波等和西班牙塞维利亚大学Cabello教授合作,利用超高精度超导量子线路实现确定性纠缠交换,以超过43个标准差的实验精度证明了实数无法完整描述标准量子力学,确立了复数的客观实在性。
可见,仅仅用实数是无法完整描述自然规律的,实际上实数仅仅能描述世界的一半,而另一半则需要虚数来描述,只有复数=实数+虚数 才能描述完整的世界。
https://baijiahao.baidu.com/s?id=1729962132685945822&wfr=spider&for=pc&searchword=%E6%94%B9%E5%8F%98%E4%B8%96%E7%95%8C%E7%9A%8417%E4%B8%AA%E5%85%AC%E5%BC%8F%E4%B9%8B%E8%99%9A%E6%95%B0%E7%9A%84%E5%A5%87%E5%A6%99%E6%97%85%E8%A1%8C 上次我们初步把虚数是怎么来的做了介绍改变世界的17个公式之虚数的奇妙旅行(一),这次
|




